STARANISO anisotropy & Bayesian estimation server.

The STARANISO Server

Anisotropy of the Diffraction Limit
and
Bayesian Estimation of Structure Amplitudes

Results obtained from the STARANISO server contributed by our users.

Example from the membrane project of Vincent Debruycker and Cédric Govaerts (Université Libre de Bruxelles).
Contributed by Pierre Legrand (Synchrotron SOLEIL).
Example from the Origin Recognition Complex project of Valerie Pye and Peter Cherepanov (Francis Crick Institute).

Contributed by Valerie Pye.
Example from Esther Ortega and José M. de Pereda (Instituto de Biología Molecular y Celular del Cáncer).
Contributed by José M. de Pereda.
Example from deposited data for PDB entry 4XYI.
Contributed by Andrew Sharff (GΦL).
Example from the lipopolysaccharide ABC transporter LptB₂FG project of Haohao Dong et al. (Sichuan University, University of East Anglia, University of Oxford & Diamond Light Source).
Contributed by Neil Paterson (DLS, 2017): Nature Communications 8, 1-11.
Example of highly anisotropic data collected on beamline I04 at Diamond Light Source.
Contributed by Lukasz Sobala and Eleanor Dodson (University of York).
Example from the β1-adrenergic G-protein-coupled receptor project of Tony Warne et al. (MRC Laboratory of Molecular Biology & University of Nottingham).
The highly anisotropic data for this example were collected in a follow-up study to (Warne et al., 2008) from complexed β1-adrenergic G-protein-coupled receptor crystals on the autonomous beam line MASSIF-1 (Bowler et al., 2015) at the ESRF Grenoble using automated crystal centering, screening and beam size matching algorithms (Svensson et al., 2015 & 2018).
Bowler, M.W., Nurizzo, D., Barrett, R., Beteva, A., Bodin, M., Caserotto, H., Delageniere, S., Dobias, F., Flot, D., Giraud, T. et al. (2015). "MASSIF-1: a beamline dedicated to the fully automatic characterization and data collection from crystals of biological macromolecules." J. Synchrotron Rad. 22, 1540-1547.
Svensson, O., Malbet-Monaco, S., Popov, A., Nurizzo, D. and Bowler, M.W. (2015). "Fully automatic characterization and data collection from crystals of biological macromolecules." Acta Crystallogr. D71, 1757-1767.
Svensson, O., Gilski, M., Nurizzo, D. and Bowler, M.W. (2018). "Multi-position data collection and dynamic beam sizing: recent improvements to the automatic data-collection algorithms on MASSIF-1." Acta Crystallogr. D74, in press.
Warne, T., Serrano-Vega, M.J., Baker, J.G., Moukhametzianov, R., Edwards, P.C., Henderson, R., Leslie, A.G.W., Tate, C.G. and Schertler, G.F.X. (2008). "Structure of a β1-adrenergic G-protein-coupled receptor." Nature 454, 486.
Contributed by Bernhard Rupp (Hofkristallamt): Rupp B. (2018) "Against Method: Table 1 — Cui Bono?".

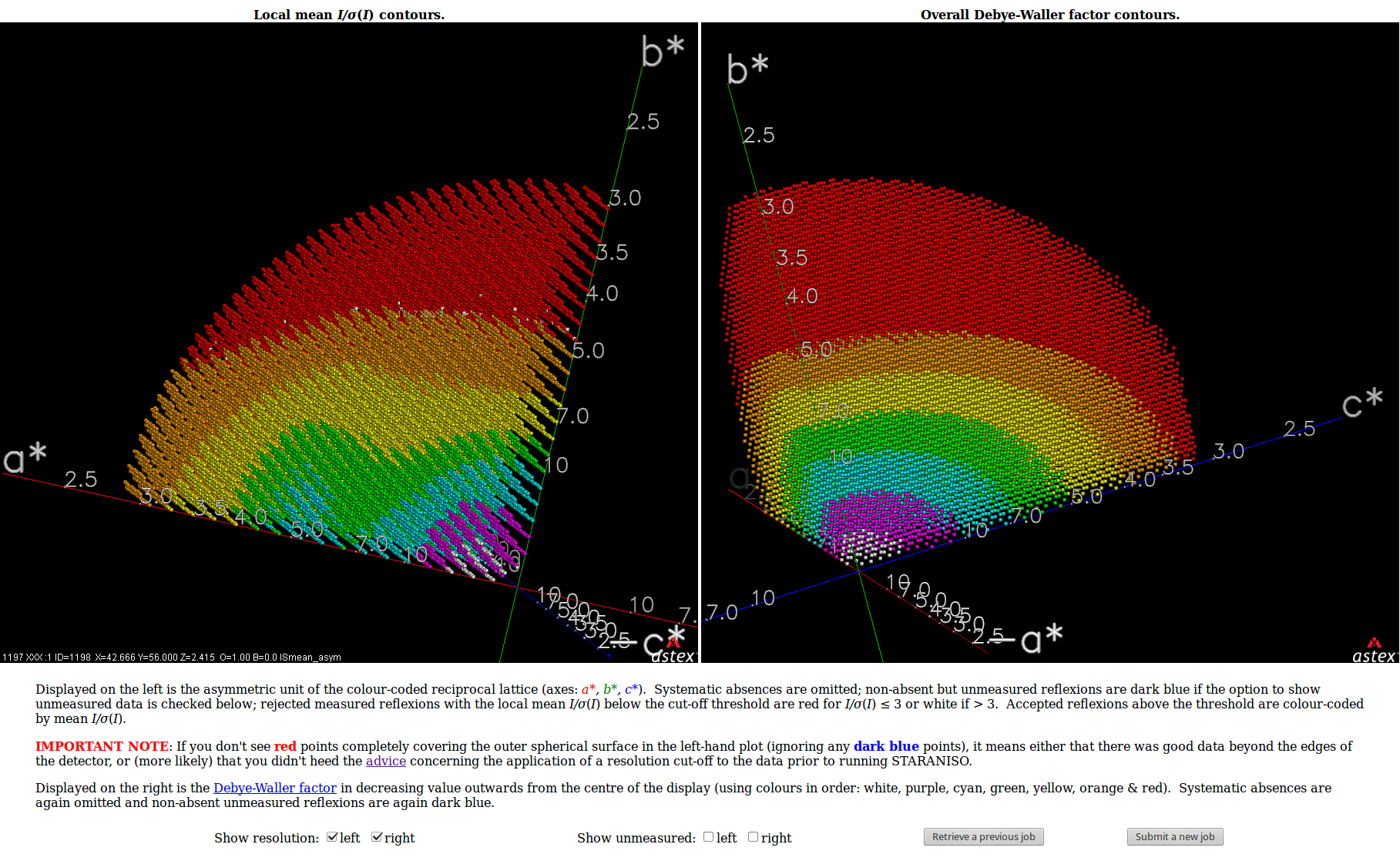
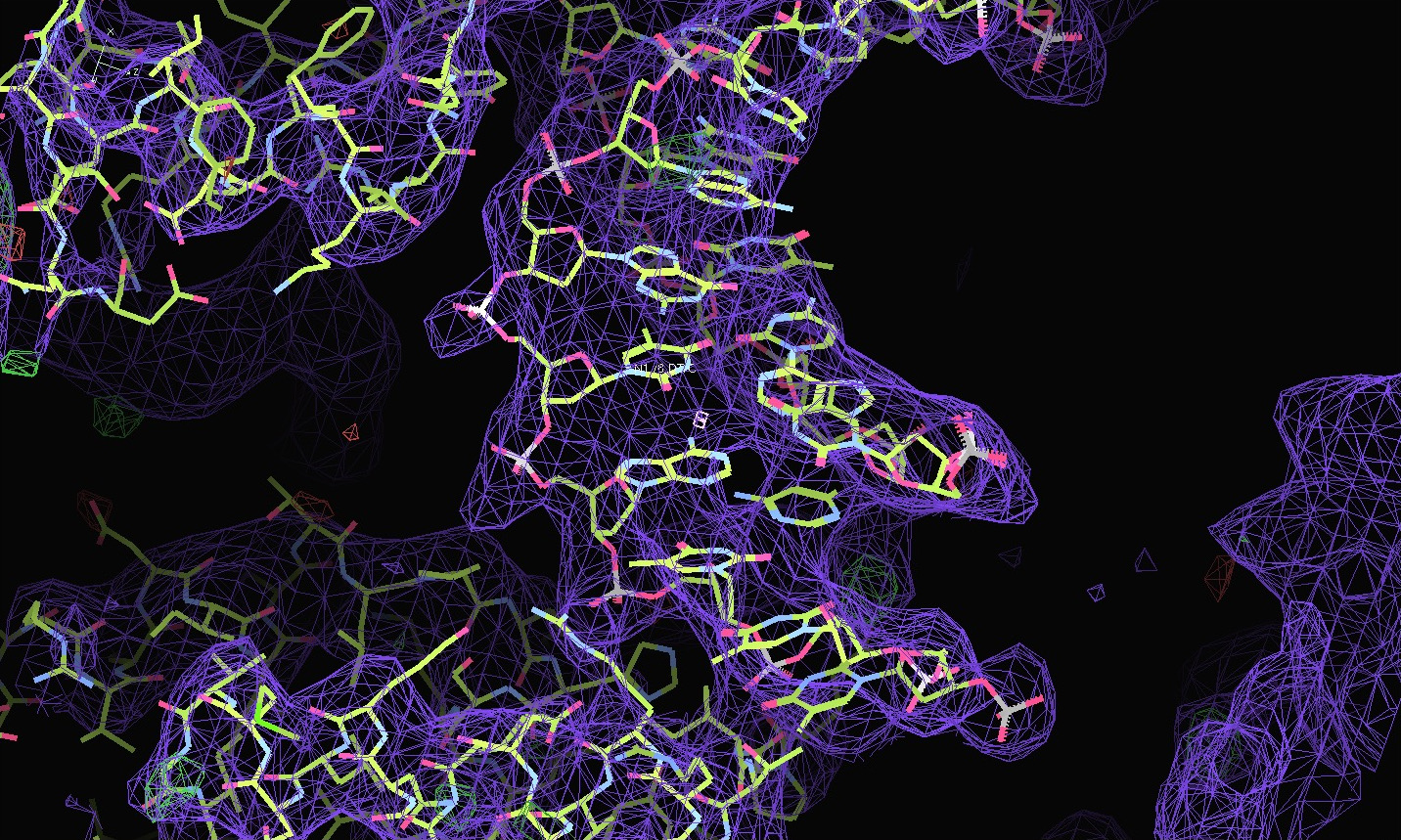
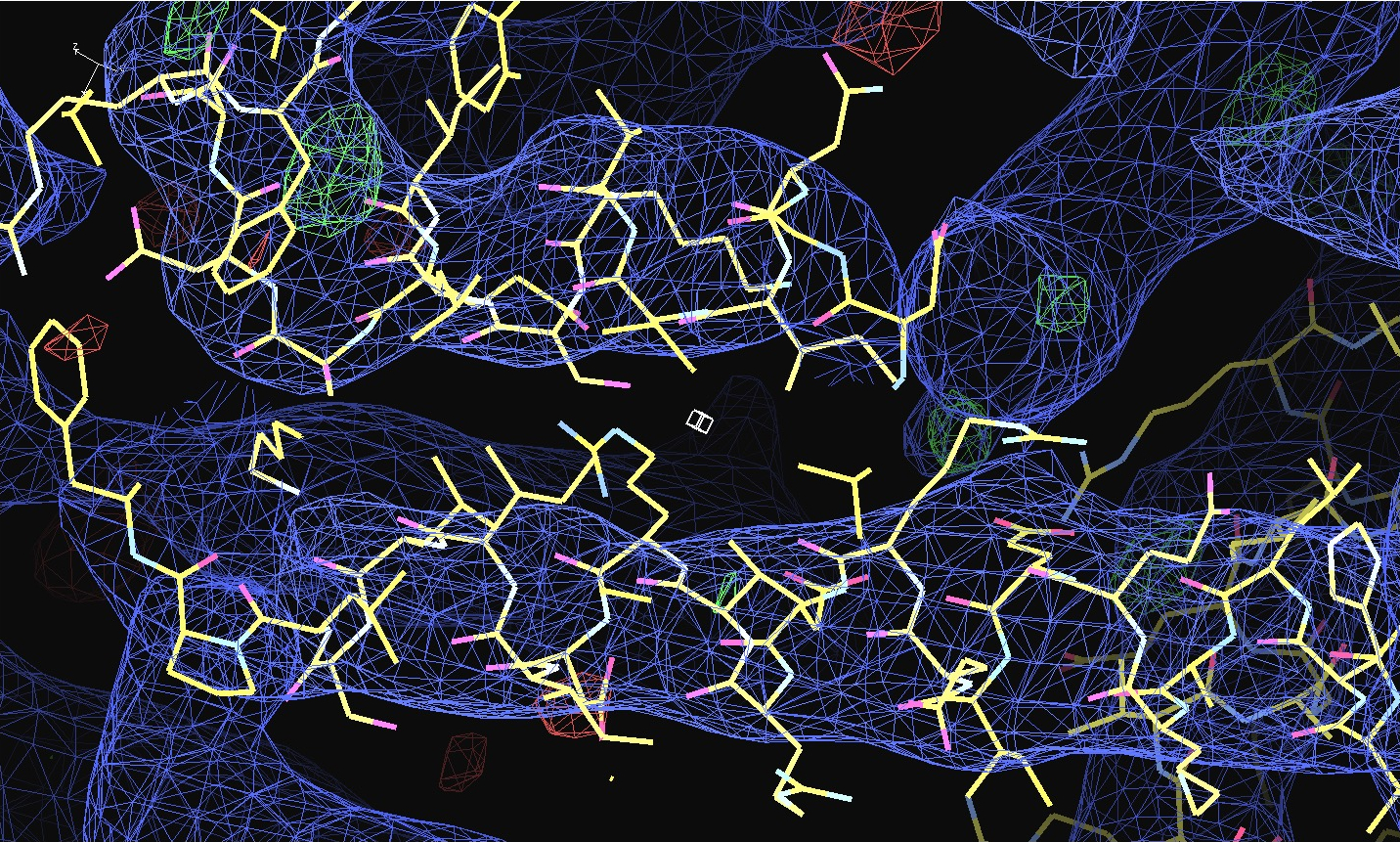
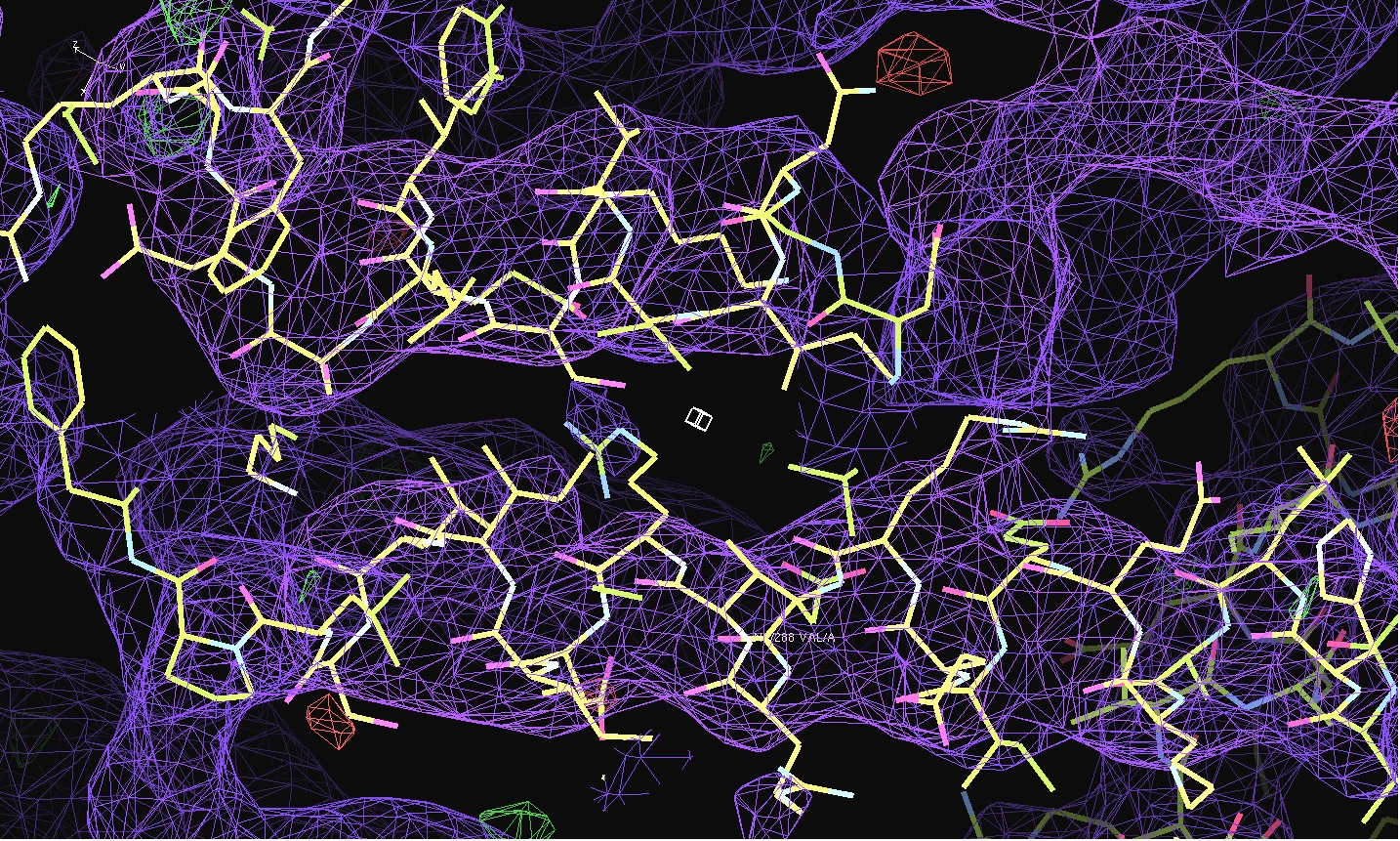
The following results were communicated to us by Pierre Legrand at Synchrotron SOLEIL (Saclay). They were obtained by him on a membrane protein project belonging to the PhD thesis of Vincent Debruycker, in Cédric Govaerts' laboratory at the Université Libre de Bruxelles.

Shown below are views of the intensity data in 3D reciprocal space provided by STARANISO and displayed by OpenAstexViewer as interactive Java applets embedded in the web page. On the left is the colour-coded distribution of the local mean value of I/σ(I), and on the right is shown the Debye-Waller factor. These indicate substantial anisotropy, as evidenced by significantly differing diffraction limits along the a*, b* and c* axes (space group: C222₁).

Shown below are the electron-density maps before (mauve) and after (blue) invocation of STARANISO. Both maps are contoured at 1.5 RMSD, corresponding to absolute contour levels of 0.1125Å^-3 for the original map and 0.1602Å^-3 for the map after treatment of the intensity data by STARANISO. The Rwork/Rfree values after the two BUSTER refinements that produced these maps are 0.3406/0.3626 and 0.3109/0.3264 respectively.

(Click the images to enlarge.)

The following results were obtained by Valerie Pye and Peter Cherepanov at the Clare Hall Laboratories, Francis Crick Institute, Potters Bar, UK. The crystals are of the Origin Recognition Complex in complex with DNA. The data were collected at the Diamond Light Source on beamline I04.

The first pair of images below shows the OpenAstexViewer displays of the intensity data in 3D reciprocal space (the local mean I/σ(I) on the left and the Debye-Waller factor on the right). The other three rows show selected portions of the electron-density map before (left column) and after (right) treatment of the intensity data by STARANISO. Both maps were contoured at 1 RMSD, corresponding to absolute contour levels of 0.0694Å^-3 for the original map and 0.0868Å^-3 for the map after treatment. The average model Biso values for the refined models are 225Å² and 160Å² respectively. The Rwork/Rfree values for the phenix.refine refinements that produced these maps are 0.3292/0.3616 and 0.3101/0.3576 respectively.

Valerie comments: "I hope you can see that the alpha helices now have features and are not just non-descript sausages; bumps can be seen for the phosphates on the DNA backbone, and beta strands have more continuous density. This should all help with refinement".

(Click the images to enlarge.)

The following results were obtained by Esther Ortega and José M. de Pereda at the Instituto de Biología Molecular y Celular del Cáncer, Salamanca, Spain. The data were collected at the European Synchrotron Radiation Facility on beamline ID14.2.

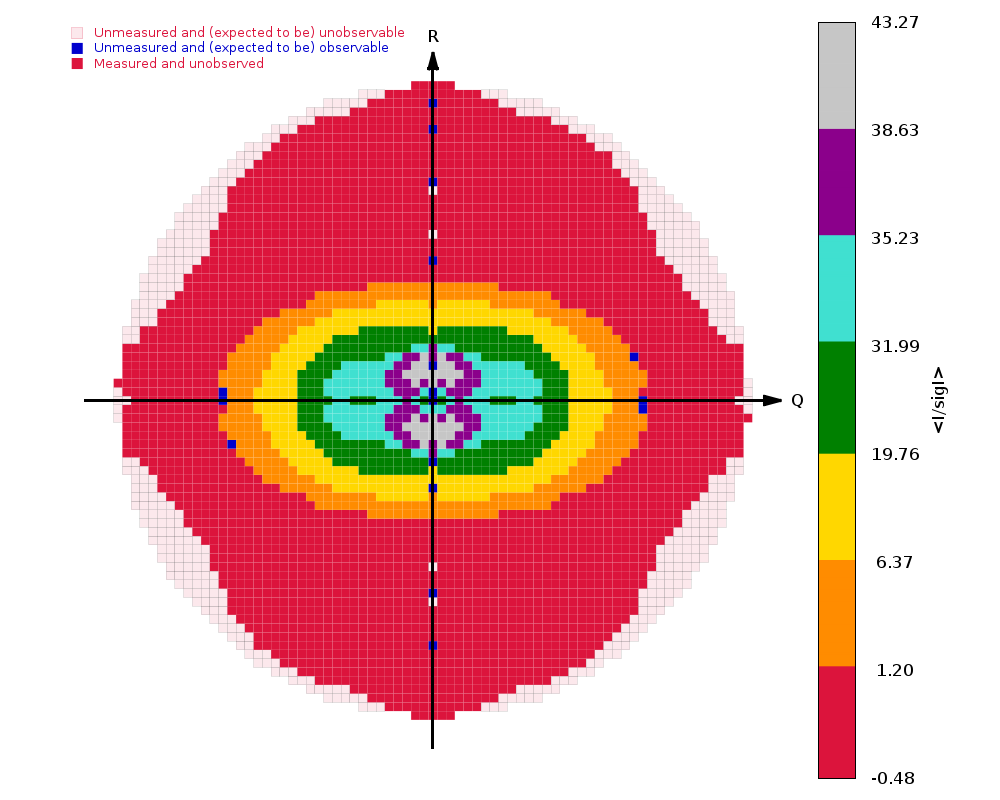
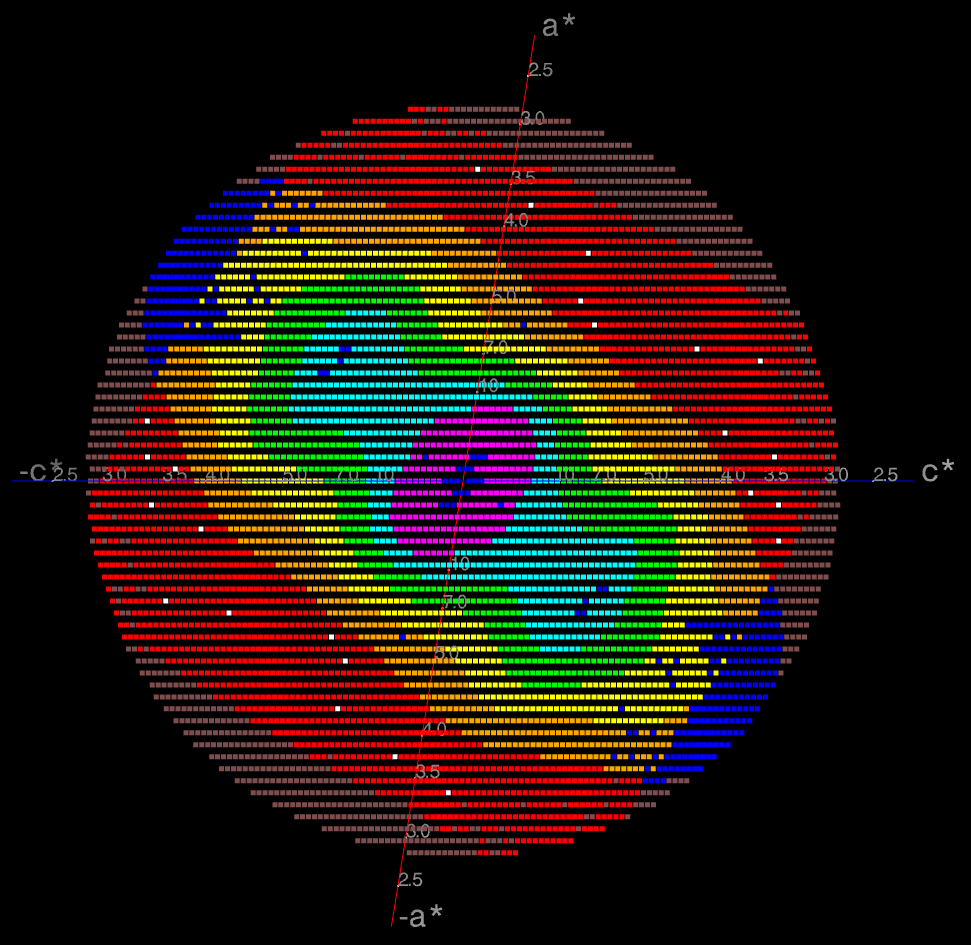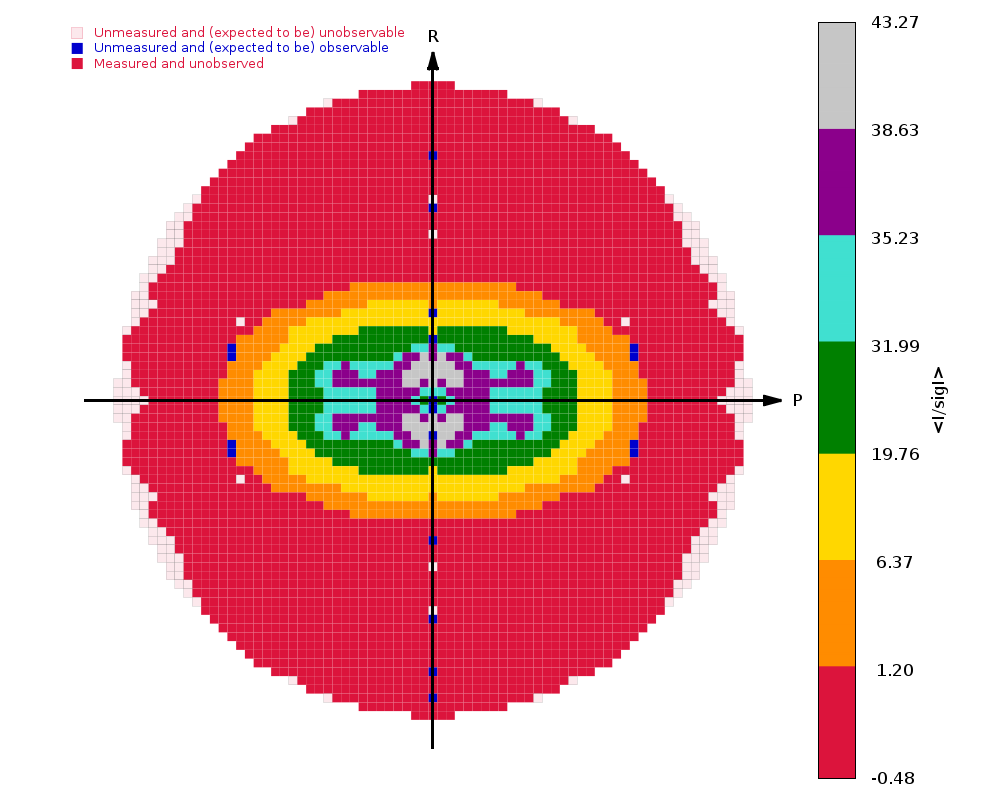
The image on the right shows the OpenAstexViewer display of the intensity data in 3D reciprocal space. The local mean value of I/σ(I) for each reciprocal lattice point within the sphere of observation is calculated by STARANISO and colour-coded: the blue points represent unobserved data, the red points represent observed data falling below the 1.2σ threshold for cut-off, and the other colours (in increasing value: orange, yellow, green, cyan, mauve, white) represent successively higher values of the mean I/σ(I). Incidentally, it can be seen that there is some truncation of some significant data (orange points) by the edges of the detector in the top left and bottom right quadrants.

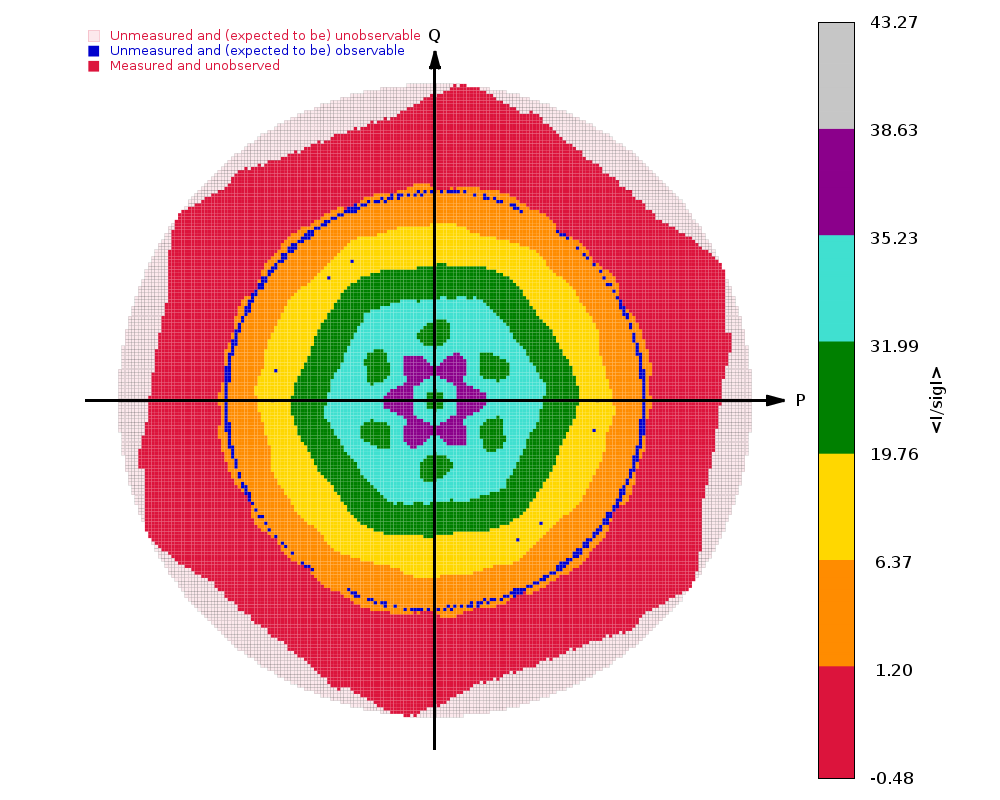
In this example the (h0l) zone of the diffraction pattern is visible: the space group is C2 in the conventional IUCr monoclinic setting with β nearest to 90^o (β = 99^o). The data are clearly highly anisotropic with the principal directions of the anisotropy clearly lying along the [-1,0,1], [0,1,0] and [1,0,1] directions. STARANISO deals optimally with this situation by truncating only the red points indicating non-significant data. Unfortunately, some other processing software make the unwarranted assumptions first that the principal directions of the anisotropy coincide with the crystal axes and second that the cut-off surface can be accurately represented by an ellipsoid (note that the principal directions and lengths provide a complete description of the anisotropy only if it is valid to assume that the cut-off surface is a well-defined shape such as an ellipsoid).

The choice of the a and c crystal axes in the monoclinic system is completely arbitrary so there's absolutely no rationale for assuming that the directions of these axes are related in any way to the principal directions of the anisotropy. In this case, because the anisotropy happens to be oriented along the diagonals in the ac plane, the diffraction limits along the crystal axes are 4.2, 3.8 and 3.6Å (i.e. apparently almost isotropic), so that an anisotropic cut-off which only took the diffraction limits along the crystal axes into account would give data with a diffraction limit of 3.6Å in the best direction, i.e. only a marginal improvement on the conventional isotropic cut-off which would give data to ~ 3.8Å. However the diffraction limits along the principal directions are actually 5.0, 3.8 and 2.4Å (latter value is a user estimate), so that the other non-optimal methods of data truncation grossly under- and over-estimate the diffraction limits in the principal directions of the anisotropy.

Note that this is not a problem that is only specific to monoclinic space groups! In general, the cut-off surface can be a completely arbitrary 3D shape that is determined not only by the anisotropy of diffraction but also by the user's choice of data-collection strategy. This means that the lowest and highest diffraction limits need not lie either along the principal directions of the assumed anisotropy ellipsoid, or in the directions of the crystal axes.

(Click the images to enlarge.)

The following results were obtained from the deposited data for PDB entry 4XYI.

The first pair of images below shows the OpenAstexViewer displays of the intensity data in 3D reciprocal space (the local mean I/σ(I) on the left and the Debye-Waller factor on the right).

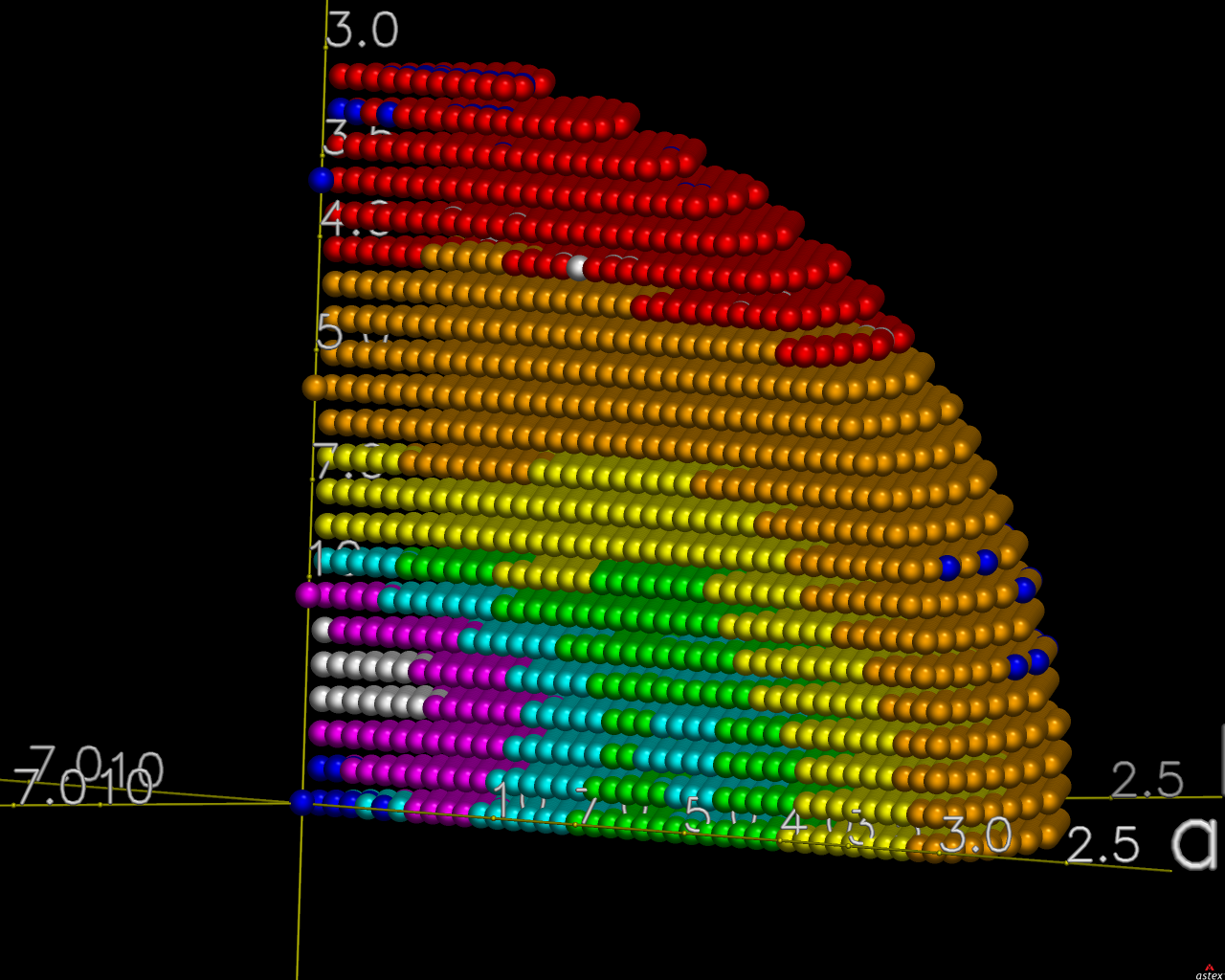
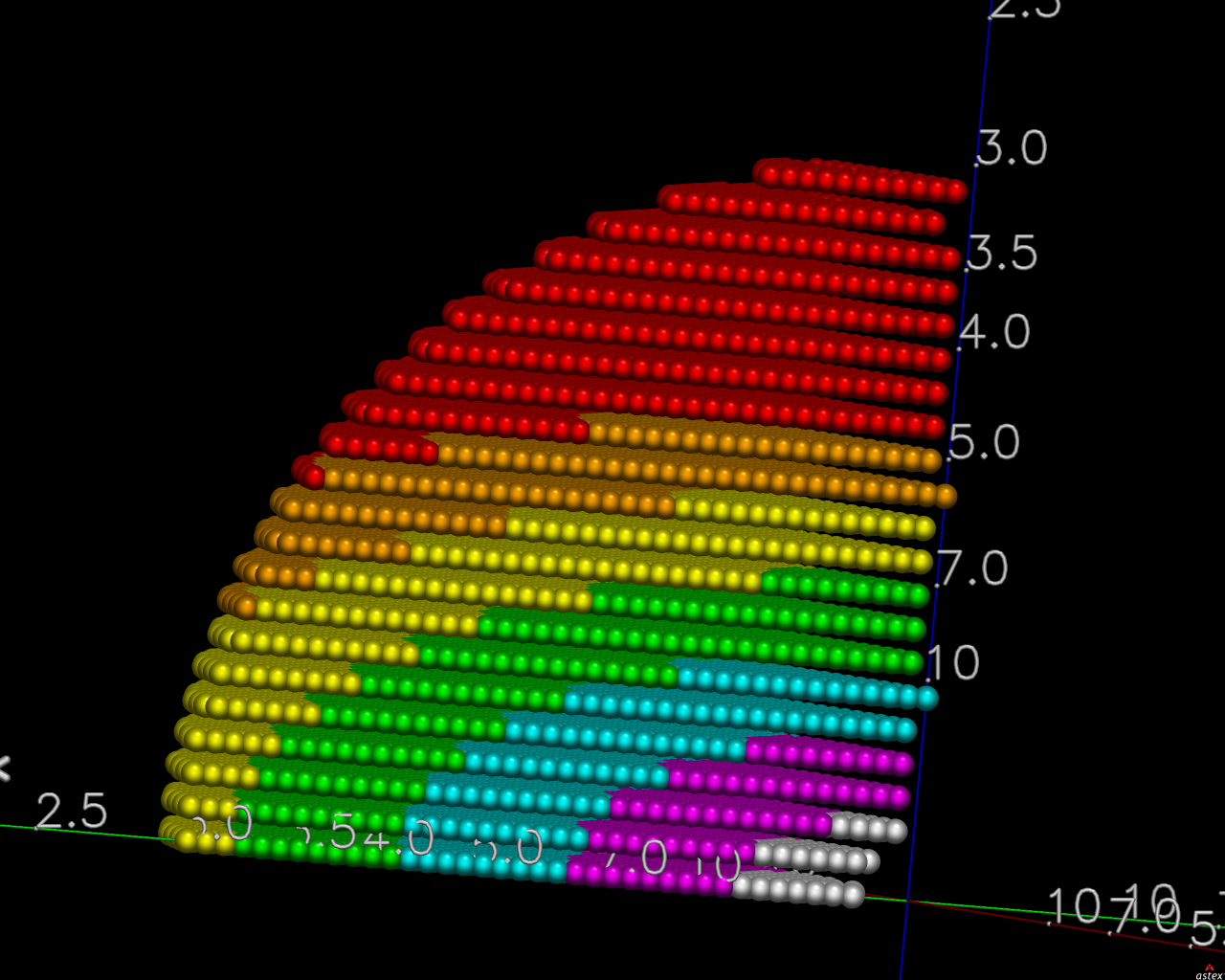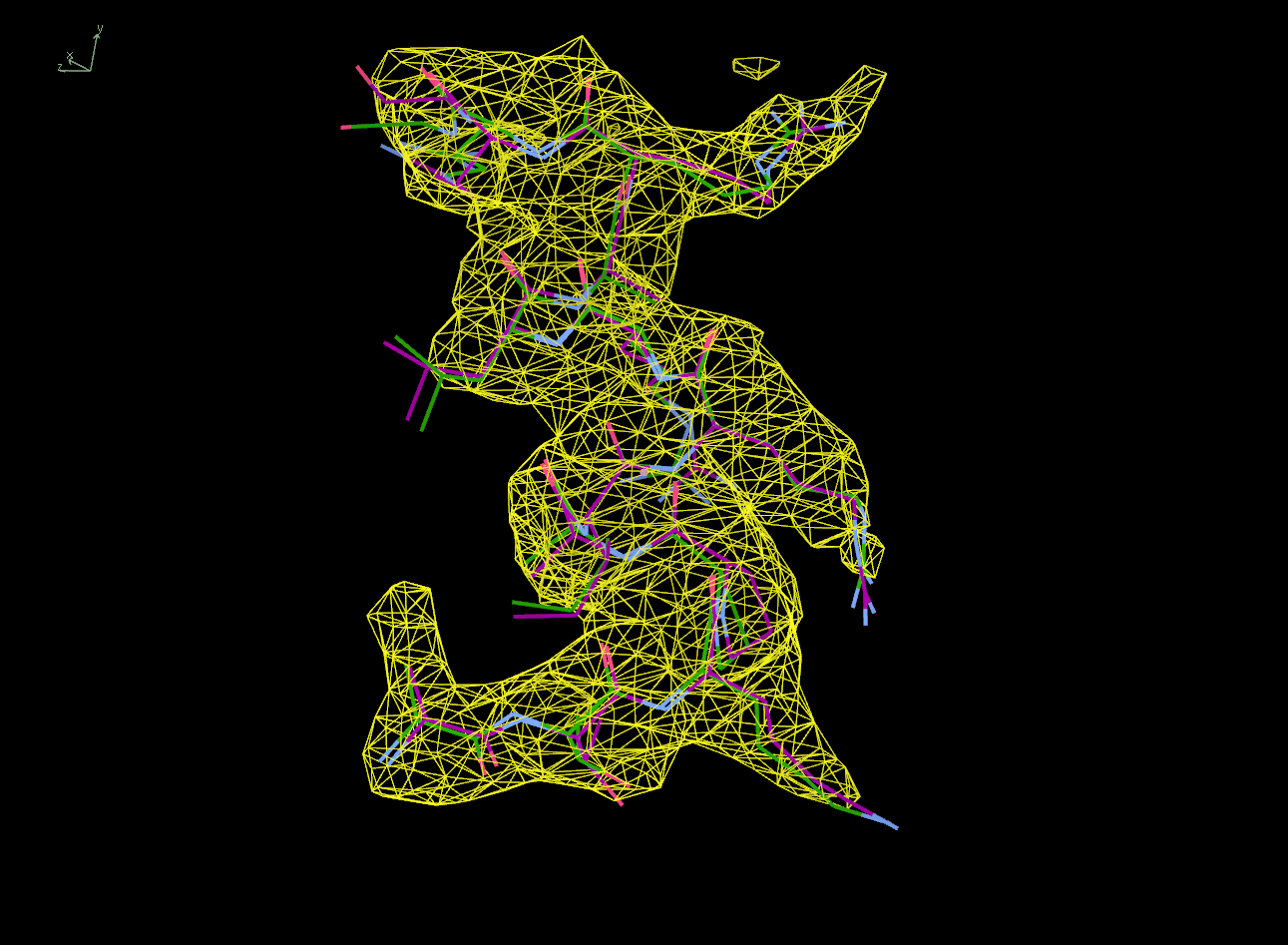
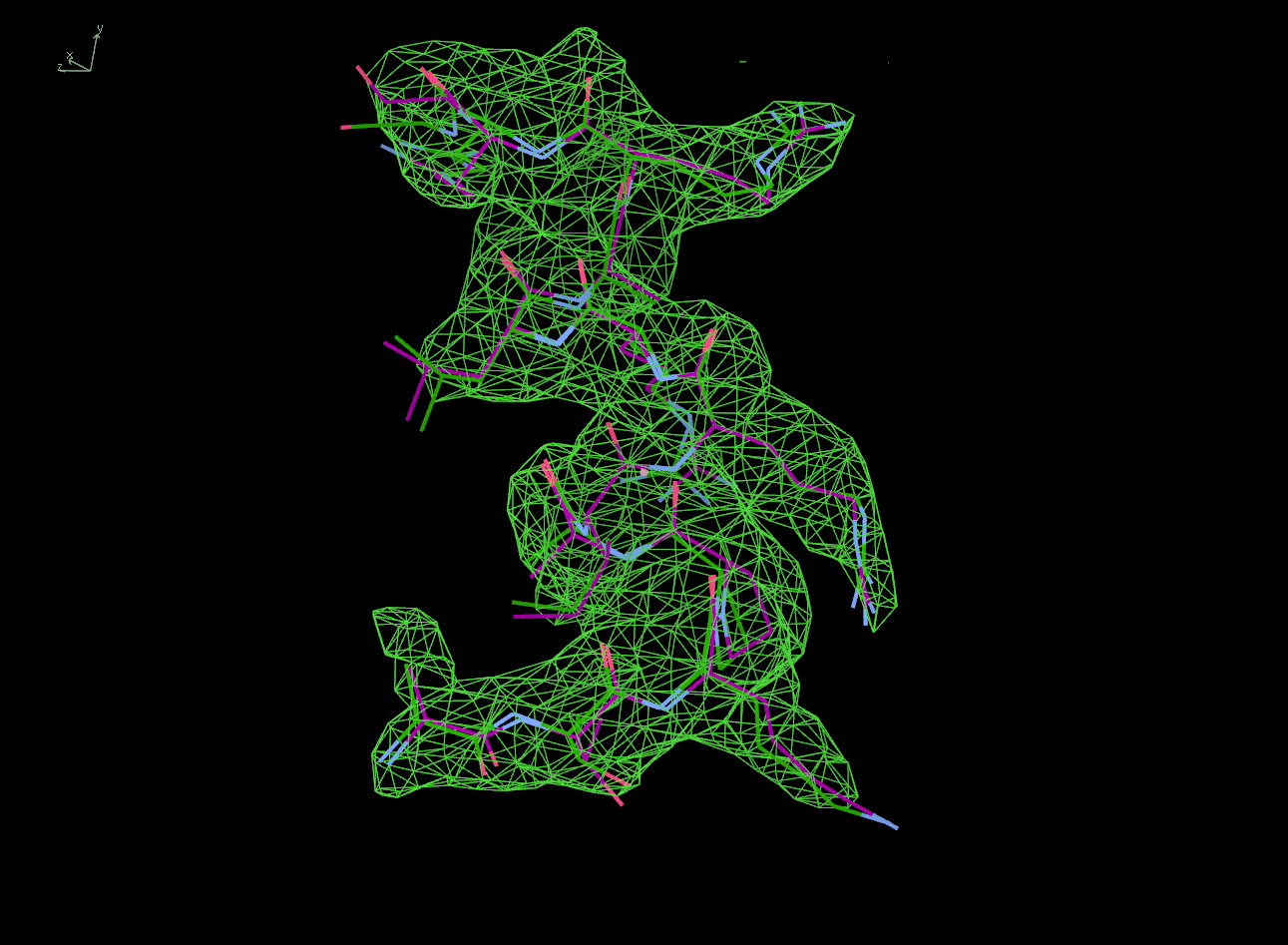
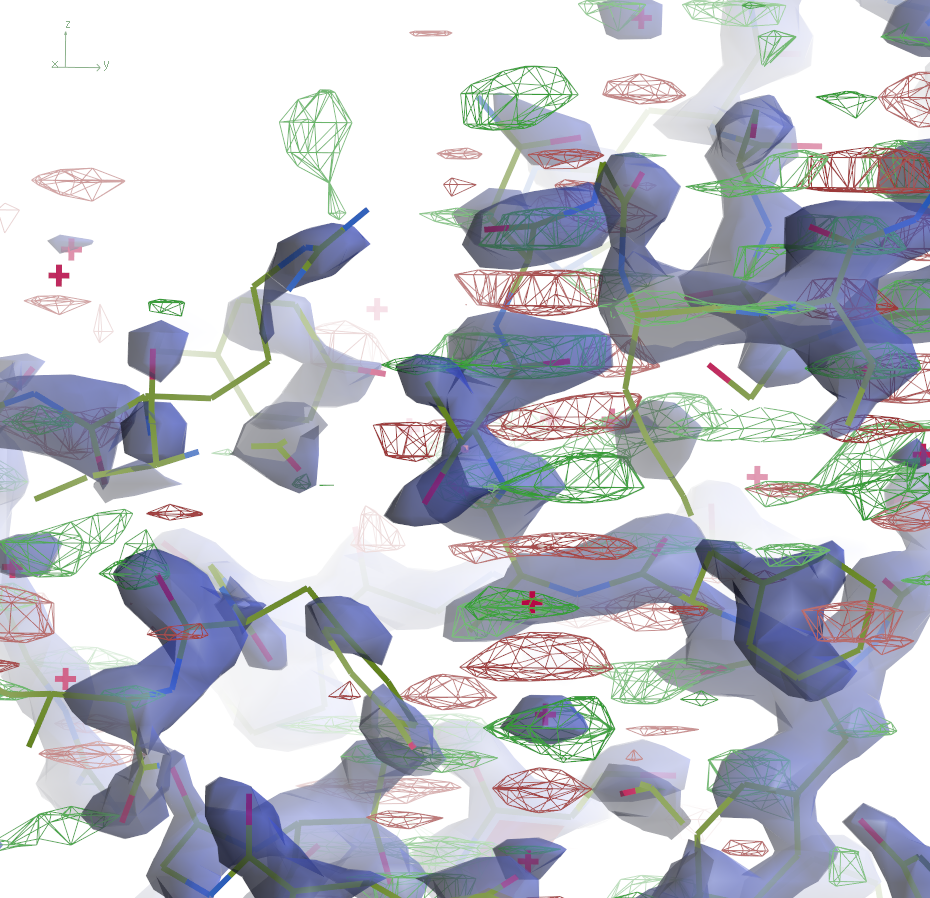
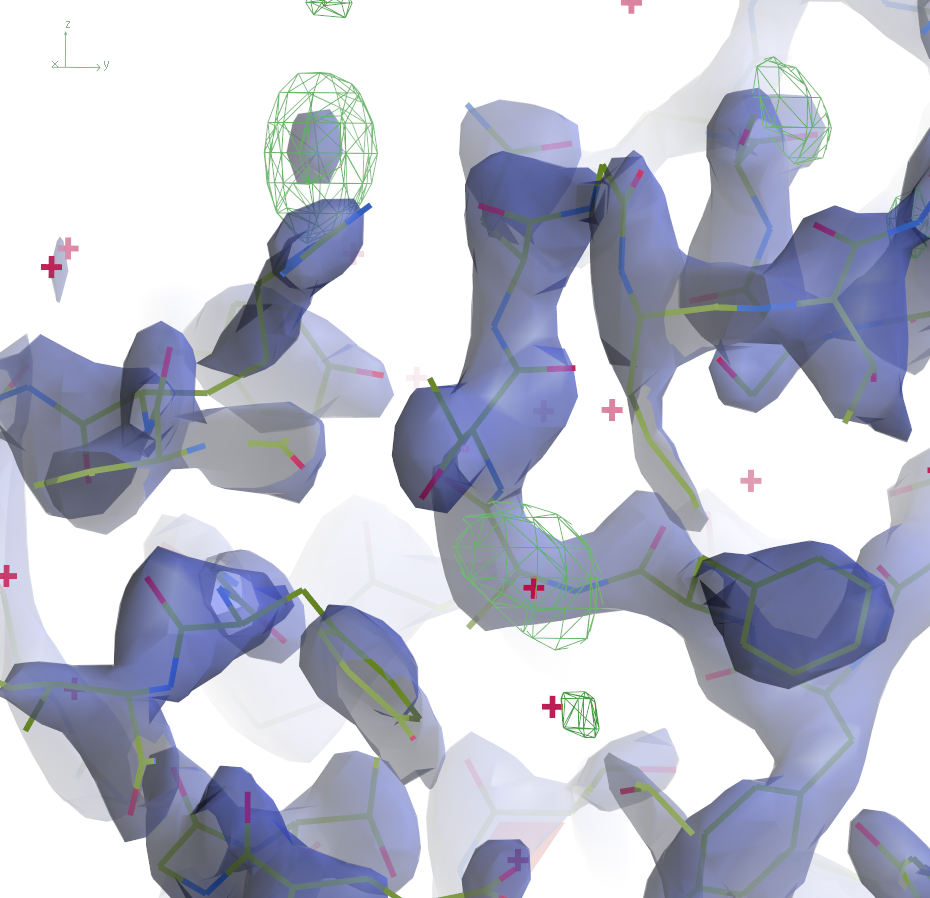
The next row of 3 images shows the model and maps for a helical peptide ligand (H4) that is an important part of the structure. The deposited model has its main-chain coloured green, while the STARANISO/BUSTER-re-refined model main-chain is coloured purple. The electron-density maps are respectively:

Left panel: the map produced by BUSTER structure-factor calculation from the deposited data;
Middle panel: the map produced by BUSTER refinement from the deposited data;
Right panel: the map produced by BUSTER refinement from the corrected data produced by STARANISO.

All maps were contoured at 1 RMSD, corresponding to absolute contour levels of 0.130Å^-3 (left), 0.124Å^-3 (middle) and 0.178Å^-3 (right).

Rwork/Rfree are 0.209/0.233 (left), 0.186/0.226 (middle) and 0.182/0.222 (right).

Note the 'BUSTER bonus' going from left to middle, and then the 'STARANISO bonus' going from middle to right.

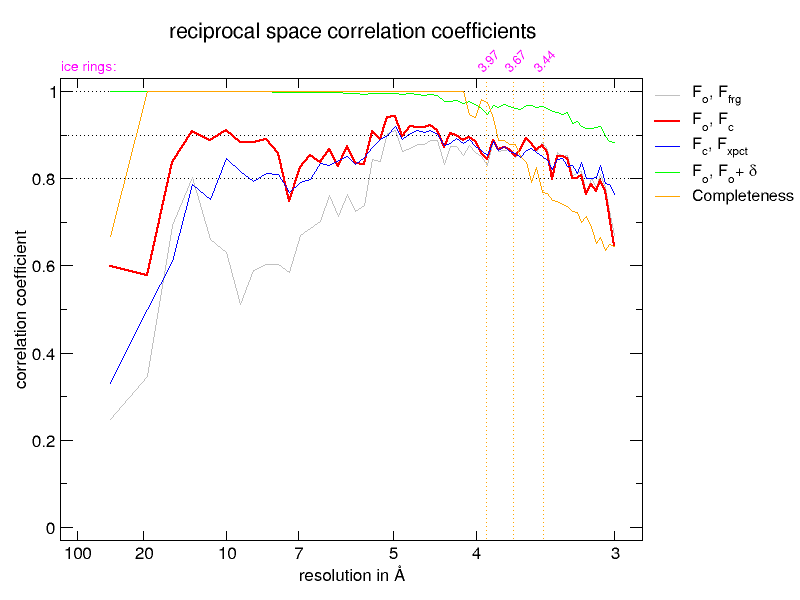
The next pair of images shows the reciprocal-space correlation plots from the BUSTER refinements, on the left before correction by STARANISO and on the right, after. Note how at high values of d* the completeness (yellow) goes down in the 'after' plot but the fit of the remaining data to the model is much better. Also the observed correlation (red) and expected correlation (blue) plots agree much better.

(Click the images to enlarge.)

The following results were communicated to us by Neil Paterson at Diamond Light Source.

Neil comments: "STARANISO has been key to solving our structure. We’ve got a severely anisotropic case that goes from around 7 Å along a* to 3.0-3.5 Å along b*/c*, with lots of artifacts in the maps. We can find the substructure using Shel-X without correction but the maps are pretty bad; once corrected it works a treat (77% solvent!)."

(Click the images to enlarge.)

The following results were communicated to us by Lukasz Sobala and Eleanor Dodson at the University of York.

₂


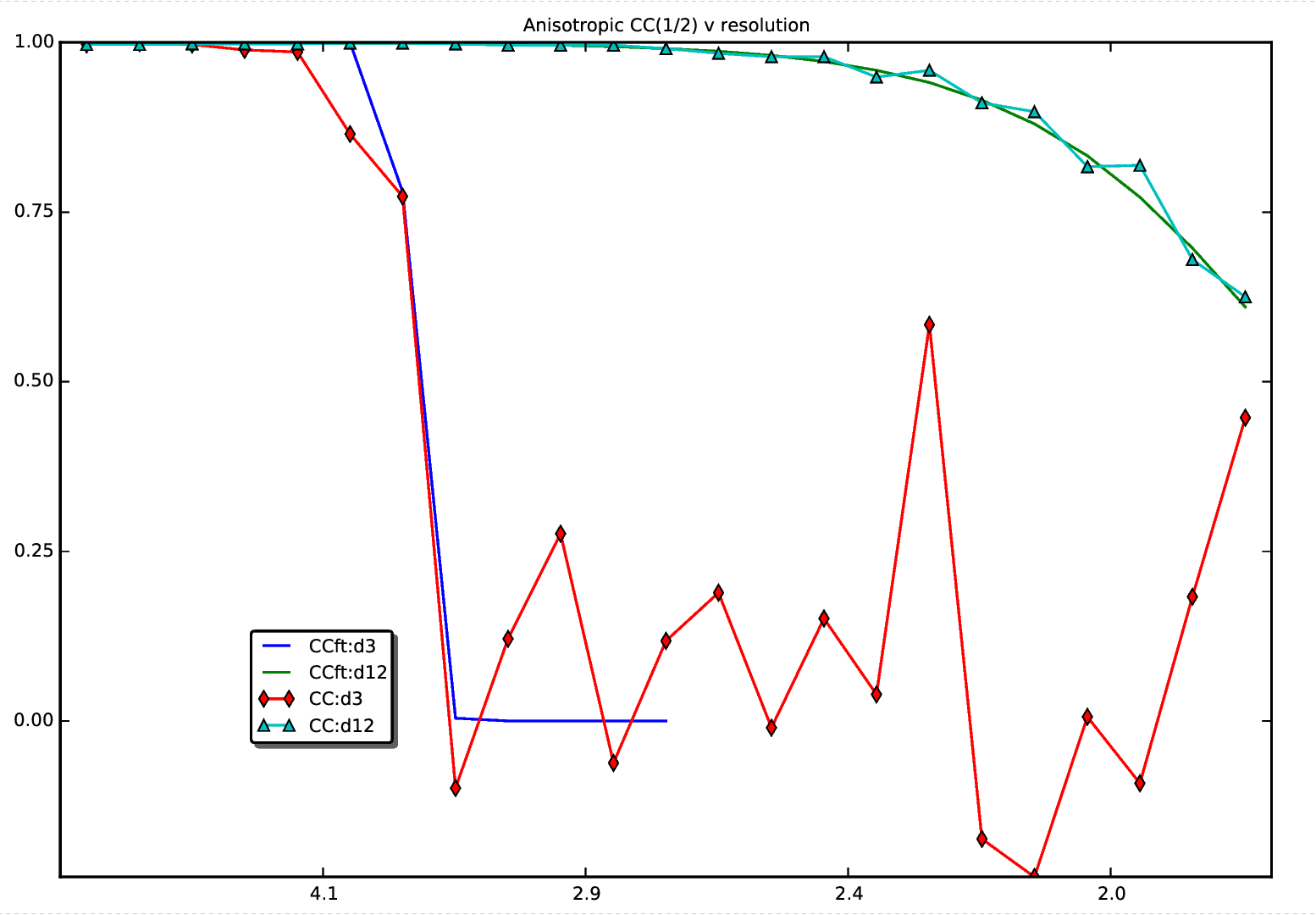
The CC(1/2) plot relates to the MTZ file used to create the original map.

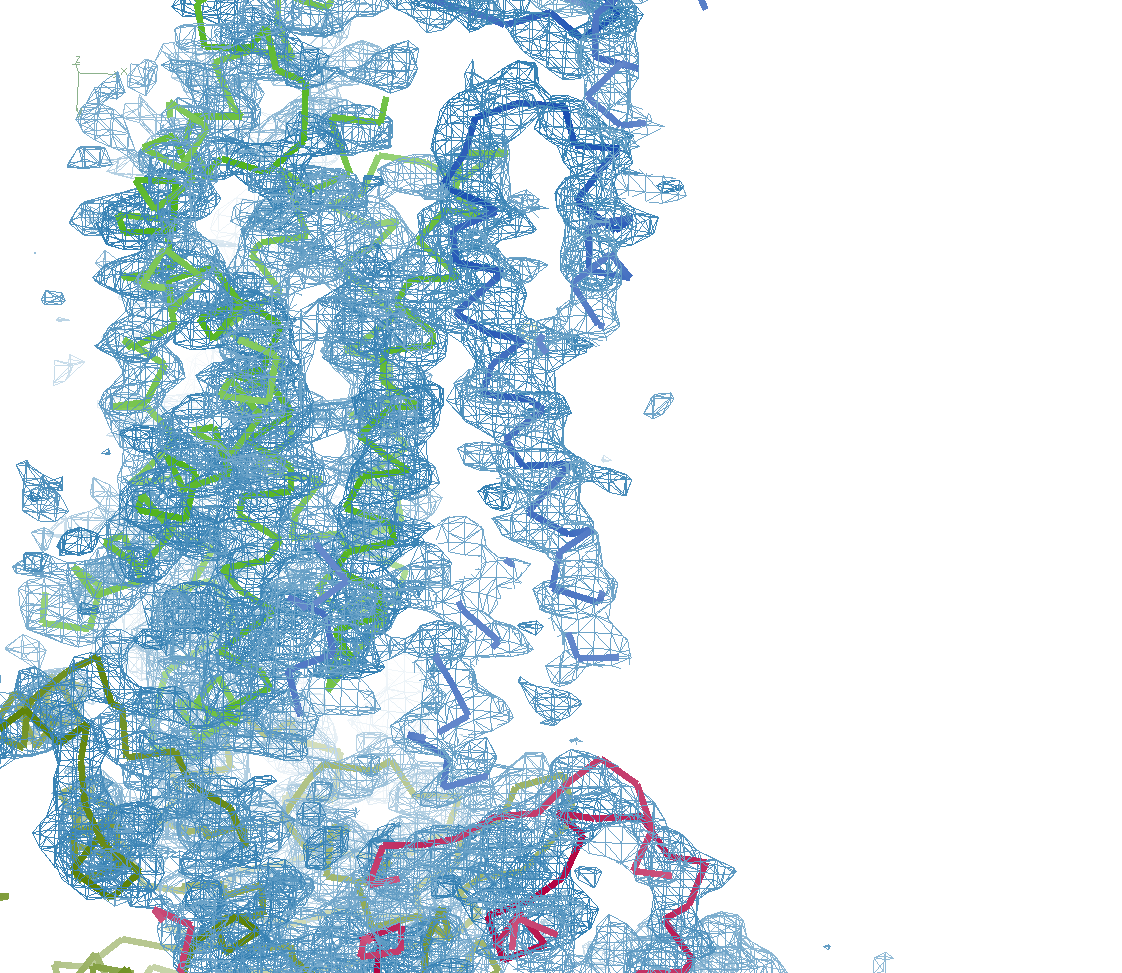
The 2mFo-DFc maps are contoured at 0.5Å^-3 and the difference maps at 0.25Å^-3. Click the images to enlarge.

The STARANISO Server

Anisotropy of the Diffraction Limit
and
Bayesian Estimation of Structure Amplitudes

Results obtained from the STARANISO server contributed by our users.

Example from the membrane project of Vincent Debruycker and Cédric Govaerts (Université Libre de Bruxelles).

Example from the Origin Recognition Complex project of Valerie Pye and Peter Cherepanov (Francis Crick Institute).

Example from Esther Ortega and José M. de Pereda (Instituto de Biología Molecular y Celular del Cáncer).

Example from deposited data for PDB entry 4XYI.

Example from the lipopolysaccharide ABC transporter LptB₂FG project of Haohao Dong et al. (Sichuan University, University of East Anglia, University of Oxford & Diamond Light Source).

Example of highly anisotropic data collected on beamline I04 at Diamond Light Source.

Example from the β1-adrenergic G-protein-coupled receptor project of Tony Warne et al. (MRC Laboratory of Molecular Biology & University of Nottingham).

The following results were communicated to us by Pierre Legrand at Synchrotron SOLEIL (Saclay). They were obtained by him on a membrane protein project belonging to the PhD thesis of Vincent Debruycker, in Cédric Govaerts' laboratory at the Université Libre de Bruxelles.

The following results were obtained by Valerie Pye and Peter Cherepanov at the Clare Hall Laboratories, Francis Crick Institute, Potters Bar, UK. The crystals are of the Origin Recognition Complex in complex with DNA. The data were collected at the Diamond Light Source on beamline I04.

The following results were obtained by Esther Ortega and José M. de Pereda at the Instituto de Biología Molecular y Celular del Cáncer, Salamanca, Spain. The data were collected at the European Synchrotron Radiation Facility on beamline ID14.2.

The following results were obtained from the deposited data for PDB entry 4XYI.

The following results were communicated to us by Neil Paterson at Diamond Light Source.

The following results were communicated to us by Lukasz Sobala and Eleanor Dodson at the University of York.

The STARANISO Server

Anisotropy of the Diffraction Limitand Bayesian Estimation of Structure Amplitudes

Results obtained from the STARANISO server contributed by our users.

Example from the membrane project of Vincent Debruycker and Cédric Govaerts (Université Libre de Bruxelles).

Example from the Origin Recognition Complex project of Valerie Pye and Peter Cherepanov (Francis Crick Institute).

Example from Esther Ortega and José M. de Pereda (Instituto de Biología Molecular y Celular del Cáncer).

Example from deposited data for PDB entry 4XYI.

Example from the lipopolysaccharide ABC transporter LptB2FG project of Haohao Dong et al. (Sichuan University, University of East Anglia, University of Oxford & Diamond Light Source).

Example of highly anisotropic data collected on beamline I04 at Diamond Light Source.

Example from the β1-adrenergic G-protein-coupled receptor project of Tony Warne et al. (MRC Laboratory of Molecular Biology & University of Nottingham).

The following results were communicated to us by Pierre Legrand at Synchrotron SOLEIL (Saclay). They were obtained by him on a membrane protein project belonging to the PhD thesis of Vincent Debruycker, in Cédric Govaerts' laboratory at the Université Libre de Bruxelles.

The following results were obtained by Valerie Pye and Peter Cherepanov at the Clare Hall Laboratories, Francis Crick Institute, Potters Bar, UK. The crystals are of the Origin Recognition Complex in complex with DNA. The data were collected at the Diamond Light Source on beamline I04.

The following results were obtained by Esther Ortega and José M. de Pereda at the Instituto de Biología Molecular y Celular del Cáncer, Salamanca, Spain. The data were collected at the European Synchrotron Radiation Facility on beamline ID14.2.

The following results were obtained from the deposited data for PDB entry 4XYI.

The following results were communicated to us by Neil Paterson at Diamond Light Source.

The following results were communicated to us by Lukasz Sobala and Eleanor Dodson at the University of York.

Anisotropy of the Diffraction Limit
and
Bayesian Estimation of Structure Amplitudes

Example from the lipopolysaccharide ABC transporter LptB₂FG project of Haohao Dong et al. (Sichuan University, University of East Anglia, University of Oxford & Diamond Light Source).