Basic Maths for Protein Crystallographers
	Phasing

An X-ray experiment allows us to measure all I(h) to some resolution limit. If we knew both |F(h)| and (h) then we could generate a map of the unit cell having peaks at and only at each atom position using the Fourier summation

This (the presence of peaks) is the fundamental property of crystal diffraction which underpins all structure solution methods.

But the phases cannot be measured directly and have to be inferred from differences between sets of intensity measurements. The experimental techniques to find them are loosely labelled as MIR, MIRAS, SIR, SIRAS, MAD, SAD:

SIR

single isomorphous replacement. Measurements are taken from a "native" protein and one "derivative" where some additional atoms have been incorporated into the lattice.

MIR

multiple isomorphous replacement. Measurements are taken from a "native" protein and several derivatives.

SIRAS

single isomorphous replacement plus anomalous differences. As above but the anomalous measurements for F(h) and F(-h) for the derivative are used.

MIRAS

multiple isomorphous replacement plus anomalous differences.

SAD

single anomalous dispersion. The "native" crystal contains some atoms which scatter anomalously, and these differences are used in a similar way to the SIR treatment.

MAD

multiple anomalous dispersion.

We need to consider the structure factor equation in more detail before discussing these.

In fact the scattering factor f(i,S) is:

f(i,S) + f'(i) + i f"(i)

where f' and f" describe the scattering from inner electron shells, which varies as a function of the wavelength, but is more or less constant at all resolutions (i.e. f"(i,S) = f"(i)). For many elements ( C, N, O in particular) f' and f" are very small at all accessible wavelengths. Others, such as S and Cl have a small but detectable component at CuK (f" ~ 0.5). In general transition elements such as Se, Br have observable f" (f" ~ 3-4) at short wavelengths. Metals and other heavy elements such as Hg, Pt, I etc. have quite large f" and f' contributions at most accessible wavelengths (at CuK f"_Hg ~ 8).

It helps to re-write the F_H(h) or F_A(h) component like this:

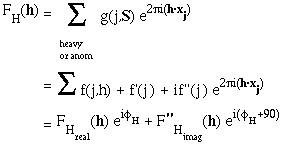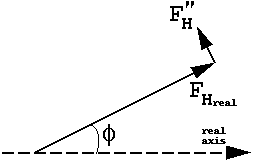The anomalous contribution is always 90 degrees in ADVANCE of the real contribution. The ratio of all |F"_H|/ |F_H| = f"(j,h)/{f(j,h) -f'(j,h)}.

Now

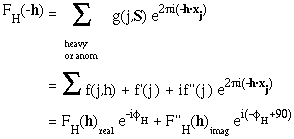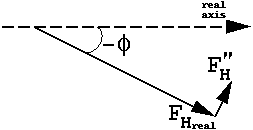which means that, although the magnitudes of F_H(h) and F_H(-h) are equal, their phases are different, and F_H(-h) is no longer the complex conjugate of F_H(h).

And since F_PH(h) = F_H(h) + F_P(h), and F_PH(-h) = F_H(-h) + F_P(-h) it follows that neither the magnitudes of |F_PH(h)| and |F_PH(-h)| are equal, nor the phase _PH(h) equal to -_PH(-h).

How does this help phasing?

Answer: In no way unless we can position the heavy (or anomalous) atoms.

If they are known, the vector F_H(h) can be calculated and from the knowledge of the three magnitudes |F_H(h)|, |F_P(h)| and |F_PH(h)| plus the phase of F_H(h), it is easy to show from a phase triangle that _P will have to equal _H±_diff.

This is often represented with "phase circles" (or phasing diagrams) or "phase triangles":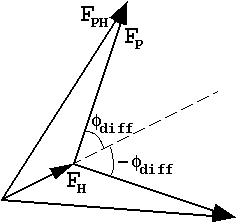

Deviation into Patterson theory

Since there are usually only a few heavy atoms associated with many protein atoms, they can usually be positioned using Pattersons or direct methods. Both these techniques require only an estimate of the magnitude of the F_H(h).

It maybe is worth summarising here the theory behind difference Pattersons.

F_PH(h) = F_H(h) + F_P(h).
The cos rule gives: |F_PH(h)|² = |F_H(h)|² + |F_P(h)|² + 2 |F_H(h)| |F_P(h)| cos_diff
where _diff is the phase between vector F_H(h) and vector F_P(h). From this we can approximate:

|F_PH(h)| = {|F_H(h|² + |F_P(h)|² + 2 |F_H(h)| |F_P(h)| cos_diff}^½ =
|F_P(h)| {1 + 2 |F_H(h)|/ |F_P(h)| cos_diff + (|F_H(h)|/ |F_P(h)|)²}^½

The binomial theorem gives (1+x)^½ ~ 1 + x/2 when x is small, so

|F_PH(h)| ~ |F_P(h)| {1 + |F_H(h)|/ |F_P(h)| cos_diff + ½(|F_H(h)|/ |F_P(h)|)²}
= |F_P(h)| + |F_H(h)| cos_diff + ½|F_H(h)|²/ |F_P(h)|

So |F_PH(h)| - |F_P(h)| ~ |F_H(h)| cos_diff + an even smaller term, providing |F_H(h)| is small compared to |F_P(h)|.
and a Patterson with coefficients (|F_PH(h)| - |F_P(h)|)² is approximately equivalent to one with coefficients (|F_H(h)| cos_diff)² = ½|F_H(h)|² (1 + cos 2_diff) (remember: cos²(x) = (1+cos(2x))/2)
The summation of ½|F_H(h)|² will give the normal Patterson distribution of vectors between related atoms while the summation of ½|F_H(h)|² cos 2_diff will generate only noise.

Deviation into Difference Fourier Theory

Similar equations explain why a Fourier summation gives full weight peaks at the atomic positions which have been included in the phasing, and peaks at about half the expected height for atoms excluded from the phasing. Say F_PH(h) = F_P(h) + F_H(h) where F_H is much smaller than F_P; i.e. only a few atoms are excluded from the phasing. Then as above

|F_PH| ~ |F_P| + |F_H| cos(_P-_H) + small terms

The Fourier summation

|F_PH| e^i_P = |F_P| e^i_P + |F_H| cos(_P-_H) e^i_P

Since cos(x) = (e^ix + e ^-ix)/2

cos(_P-_H) e^i_P = ½ (e^i_H + e^i(2_P-_H))

and the second term becomes

F_H ½(e^i_H + e^i(2_P-_H))

giving the Fourier map for the atoms contributing to F_H at half weight, plus noise, since the phase 2_P-_H is not related to these atoms at all.