Processing software: XDS(integration) Aimless(scaling)
STARANISO version: 2.4.19 (22-Nov-2024) Run on: Sat, 21 Dec 2024 20:46:12 +0100.
Using MTZ column labels: FP SIGFP
NOTE: Not doing Bayesian estimation because corrected Is or Fs were input.
Unit cell and space group: 112.891 53.030 44.352 90.00 102.46 90.00 'C 1 2 1'
Nominal diffraction range: 55.117 1.930
Input reflection count: 19401
Unique reflection count: 19175
Diffraction cut-off criterion: Local <I/sd(I)> = 1.20
Diffraction limits (Ang.) and corresponding principal axes of the ellipsoid fitted to the
diffraction cut-off surface as direction cosines relative to the orthonormal basis (standard PDB
convention), and also in terms of reciprocal unit-cell vectors:
Diffraction limit #1: 1.953 ( 0.9337, 0.0000, -0.3580) 0.974 a* - 0.226 c*
Diffraction limit #2: 1.844 ( 0.0000, 1.0000, 0.0000) b*
Diffraction limit #3: 2.072 ( 0.3580, 0.0000, 0.9337) 0.738 a* + 0.675 c*
GoF to ellipsoid (d*): 0.0241 Fraction of surface points fitted: 100.0% ( 3433 / 3433)
Number of observed reflections inside ellipsoid: 16597
Number of unobserved reflections inside ellipsoid: 1466
Number of observed reflections outside ellipsoid: 2
Lowest cut-off diffraction limit:
2.268 at reflection 9 1 18 in direction 0.447 a* + 0.050 b* + 0.893 c*
Worst diffraction limit after cut-off:
2.372 at reflection 10 0 17 in direction 0.507 a* + 0.862 c*
Best diffraction limit after cut-off:
1.930 at reflection -10 26 7 in direction -0.348 a* + 0.905 b* + 0.244 c*
NOTE that because the cut-off surface is likely to be only very approximately ellipsoidal, in part
due to variations in reflection redundancy arising from the chosen collection strategy, the
directions of the worst and best diffraction limits may not correspond with the reciprocal axes,
even in high-symmetry space groups (the only constraint being that the surface must have point
symmetry at least that of the Laue class).
Fraction of data inside cut-off surface: 86.6% ( 16599 / 19175)
Fraction of surface truncated by detector edges: 5.1% ( 68 / 1337)
Fraction of total surface above threshold truncated by cusp(s): 0.0% ( 0 / 1337)
Scale: 2.08417E-04 [ = factor to place Iobs on same scale as Iprofile.]
Beq: 72.44 [ = equivalent overall isotropic B factor on Fs.]
B11 B22 B33 B23 B31 B12
Baniso tensor: 71.88 72.19 73.27 0.00 0.92 0.00
NOTE: The Baniso tensor is the overall anisotropy tensor on Fs.
Delta-B tensor: -0.57 -0.26 0.82 0.00 0.92 0.00
NOTE: The delta-B tensor is the overall anisotropy tensor on Fs after subtraction of Beq from its
diagonal elements (so trace = 0). Neither this nor its eigenvalues shown below is used further in
any computation, including in anisotropy correction and deposition.
Eigenvalues of overall anisotropy tensor (Ang.^2), eigenvalues after subtraction of smallest
eigenvalue (as used in the anisotropy correction) and corresponding eigenvectors of the overall &
anisotropy tensor as direction cosines relative to the orthonormal basis (standard PDB convention),
and also in terms of reciprocal unit-cell vectors:
Eigenvalue #1: 71.42 0.00 ( 0.8950, 0.0000, -0.4460) 0.964 a* - 0.266 c*
Eigenvalue #2: 72.19 0.77 ( 0.0000, 1.0000, 0.0000) b*
Eigenvalue #3: 73.73 2.31 ( 0.4460, 0.0000, 0.8950) 0.825 a* + 0.565 c*
The eigenvalues and eigenvectors of the overall B tensor are the squares of the lengths and the
directions of the principal axes of the ellipsoid that represents the tensor.
Delta-B eigenvalues: -1.03 -0.26 1.28
The delta-B eigenvalues are the eigenvalues of the overall anisotropy tensor after subtraction of
Beq (so sum = 0).
Angle & axis of rotation of diffraction-limit ellipsoid relative to anisotropy tensor:
5.50 0.0000 -1.0000 0.0000
Anisotropy ratio: 0.032 [ = (Emax - Emin) / Beq ]
Fractional anisotropy: 0.016 [ = sqrt(1.5 Sum_i (E_i - Beq)^2 / Sum_i E_i^2) ]
Eigenvalues & eigenvectors of <I/sd(I)> anisotropy tensor:
1.86 0.9788 0.0000 -0.2050 0.987 a* - 0.163 c*
2.09 0.0000 1.0000 0.0000 b*
1.44 0.2050 0.0000 0.9788 0.497 a* + 0.868 c*
Eigenvalues & eigenvectors of weighted CC_1/2 anisotropy tensor:
0.274 0.9699 0.0000 -0.2436 0.984 a* - 0.178 c*
0.283 0.0000 1.0000 0.0000 b*
0.210 0.2436 0.0000 0.9699 0.570 a* + 0.822 c*
Eigenvalues & eigenvectors of <K-L divergence> anisotropy tensor:
0.579 0.9612 0.0000 -0.2759 0.982 a* - 0.191 c*
0.622 0.0000 1.0000 0.0000 b*
0.452 0.2759 0.0000 0.9612 0.624 a* + 0.781 c*
Eigenvalues & eigenvectors of <I/E[I]> anisotropy tensor:
3.83E-01 0.9977 0.0000 -0.0677 0.994 a* - 0.110 c*
3.88E-01 0.0000 1.0000 0.0000 b*
3.20E-01 0.0677 0.0000 0.9977 0.177 a* + 0.984 c*
Ranges of local <I/sd(I)>, local weighted CC_1/2, local <K-L divergence>, local <I/E[I]> and D-W factor [= exp(-4 pi^2 s.Us)]:
ISmean CChalf KLdive IEmean DWfact
0 Grey Unobservable*
1 Blue Observable*
2 Red|Pink:9 1.20 0.3000 1.038 0.956 0.0007
3 Orange 3.81 0.8988 2.304 1.084 0.0062
4 Yellow 11.46 0.9800 3.776 1.198 0.0356
5 Green 22.34 0.9869 4.703 1.319 0.1421
6 Cyan 29.14 0.9893 5.417 1.502 0.3921
7 Magenta 36.63 0.9913 7.228 1.831 0.7484
8 White 39.97 0.9919 8.624 2.166 0.9882
* Refer to GLOSSARY for explanation of terminology.
The cut-off surface uses a different color scheme:
Unmeasured points are blue (inside the fitted surface) or cyan (outside).
Unobserved points are red (in) or green (out).
Observed points are orange (in) or white (out).
The fitted surface is magenta.
Anisotropic S/N ratio: 0.699 [ = max_h | exp(4 pi^2 s_h.delta(B)s_h) - 1 | <I_h/sd(I_h)> ]
The 'anisotropic S/N ratio', unlike the 'anisotropy ratio' or the 'fractional' anisotropy shown
above, in addition to the anisotropy of the B tensor, takes both the diffraction and the local mean
I/sd(I) into account.
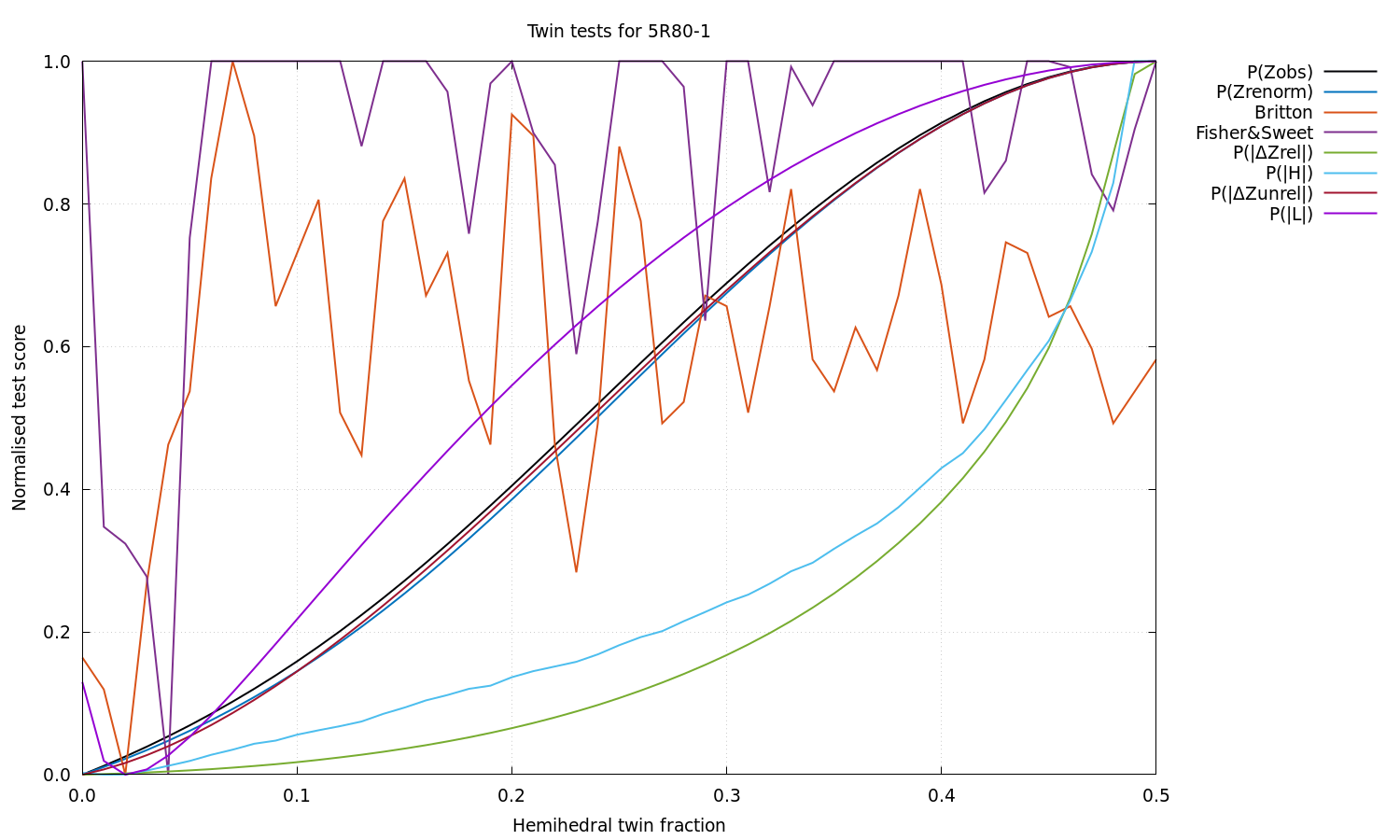
Estimated twin fraction from K-L divergence of observed acentric Z probability (before, after): 0.00 0.00
Estimated twin fraction from Britton histogram for -h-l,-k,l operator (strong, all): 0.02 0.02
Estimated twin fraction from Murray-Rust plot for -h-l,-k,l operator (strong, all): 0.00 0.08
Estimated twin fraction from weighted Fisher & Sweet plot for -h-l,-k,l operator: 0.04
Estimated twin fraction from K-L divergence of |delta-Z| probability for -h-l,-k,l operator: 0.00
Estimated twin fraction from K-L divergence of |H| probability for -h-l,-k,l operator: 0.01
Estimated twin fraction from K-L divergence of unrelated acentric |delta-Z| probability: 0.00
Padilla & Yeates L test for twinning, acentric moments of |L|:
<|L|> (normal = .500; perfect twin = .375): 0.493
<L^2> (normal = .333; perfect twin = .200): 0.322
Estimated twin fraction from K-L divergence of |L| probability: 0.02
Reference